Ssc /এসএসসি উচ্চতর গণিত সংক্ষিপ্ত সাজেশন ২০২১, ফাইনাল সাজেশন এসএসসি উচ্চতর গণিত ২০২১, Ssc Higher Math Suggestion 100% Common Guaranty, Special Short Suggestion Ssc Suggestion Higher Math 2021

বিষয়: ফাইনাল সাজেশন এসএসসি ফিন্যান্স ও ব্যাংকিং ২০২১

[ বি:দ্র:এই সাজেশন যে কোন সময় পরিবতনশীল ১০০% কমন পেতে পরিক্ষার আগের রাতে সাইডে চেক করুন এই লিংক সব সময় আপডেট করা হয় ]

চিত্রে একটি পঞ্চভুজেরর শীষ বিন্দুগুলাে A(-12,10) 𝐵(-4,-2), 𝐶(6, -8), 𝐷(t, 3),𝐸(𝑡, ৩), 𝐹(6, 8) এবং শীষ বিন্দুগুলাে ঘড়ির কাঁটার বিপরীতে দিকে আবতিত।

ক)B ও E বিন্দুর সংযোজক রেখা x অক্ষের ধনাত্মক দিকের সাথে কত ডিগ্রি কোণ উৎপন্ন করে তা নির্ণয় করো।
খ) ABCDE পঞ্চভুজের ক্ষেত্রফল 236 বর্গ একক হলে, D বিন্দুর স্থানাঙ্ক নির্ণয় করো।
গ) F বিন্দুর স্থানাঙ্ক (-2,4) হলে, সুবিধামতো একক নিয়ে ABCF চতুর্ভুজ টি আক এর প্রকৃতি নির্ণয় করো।
ঘ) P(k,h) ও Q(k,h) বিন্দু দুইটি যথাক্রমে AB ও AE রেখার অপর অবস্থিত হলে PQ সরলরেখার সমীকরণ নির্ণয় করো।

উত্তর : লিংক

মিনার বয়স রাজুর বয়সের দ্বিগুণ অপেক্ষা 1 বছর কম। মিনার বয়স y বছর ও রাজুর বয়স ৫ বছর এবং তাদের বয়সের সম্পর্ক একটি সমীকরণ দ্বারা প্রকাশ করা যায়। x ও y কে চলক বিবেচনা করে সমীকরণটি থেকে যে সরলরেখা পাওয়া যায় উক্ত সরলরেখার উপর A(m,5) একটি বিন্দু। সরলরেখাটি x ও y অক্ষদ্বয়কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।

ক) A বিন্দুর স্থানাঙ্ক নির্ণয় কর ও সরলরেখাটি অঙ্কন করে A বিন্দুটি চিহ্নিত কর। (সমীকরণ নির্ণয় করে A(m, 5) বিন্দু দ্বারা সিদ্ধ করবে ও m এর মান নির্ণয় করবে সুবিধামত | একক নিয়ে গ্রাফ পেপারে সরলরেখাটি আঁকবে ও A বিন্দুটি চিহ্নিত করবে।) |
খ) R(h, -2) বিন্দুটি P ও Q বিন্দু থেকে | সমদূরবর্তী হলে, h এর মান নির্ণয় কর। 1 (P ও Q বিন্দুর স্থানাঙ্ক নির্ণয় করবে। দূরত্ব নির্ণয়ের সূত্র ব্যবহার করে h এর মান নির্ণয় | করবে।)
গ) P Q ও S(2a, a -2) বিন্দুত্রয় সমরেখ হলে, S বিন্দুর স্থানাঙ্ক নির্ণয় কর। (ক্ষেত্রফলের বা ঢালের সূত্র ব্যবহার করে ১ বিন্দুর স্থানাঙ্ক নির্ণয় করবে।)।
ঘ) (2) বিন্দুগামী ও AP রেখার সমান্তরাল সরলরেখার সমীকরণ নির্ণয় কর। (AP রেখার ঢাল নির্ণয় করে (2) | বিন্দুগামী সরলরেখার সমীকরণ নির্ণয় করবে।)

উত্তর : লিংক

মি. রাতুল প্রতিদিন প্রাতঃভ্রমনে দুই কিলােমিটার পরিধিবিশিষ্ট একটি বৃত্তাকার পার্ক সমবেগে একবার প্রদক্ষিণ করেন । তিনি সকাল 6:45 মিনিটে প্রদক্ষিণ শুরু করে সকাল 7:25 মিনিটে শেষ করেন;

নির্দেশনা (সংকেত/ধাপ/পরিধি):

ক) মি. রাতুল ঠিক সকাল 7:00 পর্যন্ত যে পথ অতিক্রম করেন তা পার্কটির কেন্দ্রে কত ডিগ্রি কোণ উৎপন্ন করে নির্ণয় কর;

খ) প্রদক্ষিণ শুরুর সময় ঘড়িতে ঘন্টার কাঁটা এবং মিনিটের কাঁটার মধ্যবর্তী কোণের মান কত ছিল তা রেডিয়ানে প্রকাশ কর;

গ) পার্কের পরিধি যাই হােক না কেন পার্কের সীমানা বরাবর এর ব্যাসার্ধের সমান পথ হাঁটলে কেন্দ্রে উৎপন্ন কোণের পরিমাণ পরিবর্তন হবে কিনা সে সম্পর্কে যুক্তি দাও;

উত্তর : লিংক

[ বি:দ্র: নমুনা উত্তর দাতা: রাকিব হোসেন সজল ©সর্বস্বত্ব সংরক্ষিত (বাংলা নিউজ এক্সপ্রেস)]

অসীম ধারা সংক্রান্ত সমস্যা সমাধান তুমি একটি আজব দেশে ঘুরতে গিয়েছ। সেখানে দেখলে একটি গাছের নিচে পাশাপাশি ১০ টি বাক্স রাখা আছে। প্রতিটি বাক্সের গায়ে একটি করে ভগ্নাংশ লেখা আছে।

বাক্সগুলাে এমনভাবে সাজানাে আছে যেন ভগ্নাংশগুলাের ক্রম নিচের চিত্রের মত দেখা যায়।

⅔, 22/33, 222/333,……. a/b ভগ্নাংশগুলাের যােগফলকে লঘিষ্ঠ আকারে প্রকাশ করলে যে ভগ্নাংশটি পাওয়া যায় তা হলাে ৷

ক) a/b এর লঘিষ্ঠ আকার নির্ণয় কর।
খ)m/k নির্ণয় কর।
গ) na, k, mk, 1,k, … | অনুক্রমের সাধারণ পদ নির্ণয় কর। (1,0,1,0,1,0, … এবং 0.1.0,10,1, … অনুক্রম দুইটির সাধারণ পণ ব্যবহার করবে!)
ঘ) বাক্সের সংখ্যা অসীম হলে প্রতিটি বাক্সের গায়ে প্রাপ্ত ভগ্নাংশের হরগুলাে দ্বারা তৈরিকৃত ধারার n তম আংশিক সমষ্টি নির্ণয় কর। ৩) যেকোনাে একটি বাক্সের ভগ্নাংশকে আবৃত্ত দশমিকে রূপান্তর করে অনন্ত গুণােত্তর ধারায় প্রকাশ কর। অত:পর ধারাটির অমীমতক সমটি (যদি থাকে), তবে তা নির্ণয় কর।

উত্তর : লিংক

X অক্ষের ধনাত্মক দিক বরাবর OX রশ্মির অবস্থান। OX রশ্মির সাপেক্ষে ঘূর্ণায়মান অপর একটি রশ্মি OY, Oবিন্দুতে ∠XOY = Ø উৎপন্ন করে। OYএর উপর Pযেকোনাে বিন্দু।
শিখনফল/ বিষয়বস্তু:
১. চারটি চতুর্ভাগে ত্রিকোণমিতিক অনুপাতসমুহের চিহ্ন নির্দেশ করতে পারবে।
২. অনুর্ধ্ব 2π কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় করতে পারবে।
৩.-Ø কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় করতে পারবে।
৪. পূর্ণসংখ্যা n(n ≤ 4)এর জন্য (nπ/2 ± Ø)কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় ও প্রয়ােগ করতে পারবে।
নির্দেশনা (সংকেত/ধাপ/পরিধি):
(ক) P এর স্থানাঙ্ক (20, -21) হলে cotø+ cosecø/sinø+cosø এর মান নির্ণয় কর।
(খ) P এর স্থানাঙ্ক (-√3, -21) হলে দেখাও যে, (cotø- cosecø+1)(1 +cosø) = 3-√3/2;
(গ) P এর স্থানাঙ্ক (√3 -1) হলে ∑■(6@n) =1 cos^2(2n-1)øএর মান নির্ণয় কর।
(ঘ) o ≤ ø ≤ 2π এর জন্য Cos^4ø – sin^4ø = 6cos^2ø – 2) (1 – 2sinø) সমীকরণটি সমাধান করে OY রশ্মির অবস্থান কোন কোন চতুর্ভাগে তা উল্লেখ কর।

সাজেশন সম্পর্কে প্রশ্ন ও মতামত জানাতে পারেন আমাদের কে Google News <>YouTube : Like Page ইমেল : assignment@banglanewsexpress.com

উত্তর : লিংক

ক) k এর মান নির্ণয় কর। |
খ) যদি 2y -X – 6 = 0 সরলরেখাটি CD রেখাকে P বিন্দুতে এবং y ও X অক্ষকে যথাক্রমে R ও Q বিন্দুতে ছেদ করে, তবে APQC এর ক্ষেত্রফল নির্ণয় কর।
গ) R বিন্দুগামী ও CD এর সমান্তরাল রেখার ] সমীকরণচিত্রাঙ্কক্ষ কর;
ঘ) ACQE একটি সামান্তরিক হলে, E বিন্দুর স্থানাঙ্ক নির্ণয় করে xy সমতলে ( হক কাগজে) বিন্দু পাতন পূর্বক সামান্তরিকটি অঙ্কন কর এবং তিনটি ভিন্ন উপায়ে এর ক্ষেত্রফল নির্ণয় কর।

উত্তর : লিংক

৯ম শ্রেণির উচ্চতর গণিত এ্যাসাইনমেন্ট ৩য় সপ্তাহ ২০২১

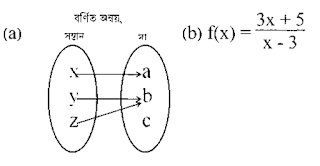
(ক) বর্ণিত অন্বয়টি ফাংশন হলে তা কী ধরনের ফাংশন যুক্তিসহ উল্লেখ কর।
(খ) (a) এর বিপরীত ফাংশন সম্ভব কিনা তা যুক্তিসহ উপস্থাপন কর।
(গ) (b) এর ক্ষেত্রে x ≠ 3 এর জন্য ফাংশনটি এক-এক এবং সার্বিক কিনা তা যুক্তি দিয়ে নিজস্ব মতামত উপস্থাপন কর।

উত্তর : লিংক

(ক) BC বরাবর A বিন্দুর লম্ব অভিক্ষেপের দৈর্ঘ্য কত তা যুক্তিসহ উল্লেখ কর।

(খ) AC এর দৈর্ঘ্য নির্ণয় কর।

(গ) দেখাও যে, PQ²< PR² + QR²

নির্দেশনা (সংকেত/ধাপ/পরিধি):

উচ্চতর গণিত পাঠ্যবইয়ের তৃতীয় অধ্যায়ে আলােচিত লম্ব অভিক্ষেপ ও পিথাগােরাসের উপপাদ্যের বিস্তৃতির সম্পর্কে ধারণা নিয়ে সমস্যাটি সমাধান। করবে। তাই সম্পূর্ণ অধ্যায়টি ভালােভাবে পড়ে সমস্যাটি সমাধান কর।

উত্তর : লিংক

একটি বৃত্তাকার হেলিপ্যাড (হেলিকপ্টার অবতরণের স্থান) এর ব্যাসের দুই প্রান্ত পৃথিবীর কেন্দ্রে 16″ কোণ উৎপন্ন করে। পৃথিবীর ব্যাসার্ধ 6440 কিলােমিটার। কোনাে ব্যক্তি ঘন্টায় 10 কিলােমিটার বেগে সাইকেল চালিয়ে 10 মিনিটের মধ্যে ঐ হেলিপ্যাডটি প্রদক্ষিণ করতে পারবে কিনা সে সম্পর্কে তােমার যুক্তি উপস্থাপন কর।

নির্দেশনা :

উচ্চতর গণিত পাঠ্যবইয়ের ৮ম অধ্যায়ে | আলােচিত রেডিয়ান পরিমাপ ও ডিগ্রী পরিমাপের পারস্পরিক সম্পর্ক এবং বৃত্তের কোনাে চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণের সাথে ঐ বৃত্তচাপের পারস্পরিক সম্পর্কে | ধারণা নিয়ে সমস্যাটি সমাধান কর।

উত্তর : লিংক

২০২১ সালের এসএসসি উচ্চতর গণিতমডেল টেস্ট- ১ লিংক

২০২১ সালের এসএসসি উচ্চতর গণিতমডেল টেস্ট- ২ লিংক

২০২১ সালের এসএসসি উচ্চতর গণিতমডেল টেস্ট- ৩ লিংক

২০২১ সালের এসএসসি উচ্চতর গণিতমডেল টেস্ট- ৪ লিংক

২০২১ সালের এসএসসি পরীক্ষার উচ্চতর গণিত সিলেবাস pdf

সবার আগে সাজেশন আপডেট পেতে Follower ক্লিক করুন

সাজেশন সম্পর্কে প্রশ্ন ও মতামত জানাতে পারেন আমাদের কে Google News <>YouTube : Like Page ইমেল : assignment@banglanewsexpress.com