what are the measures of central tendency in statistics
central tendency in statistics, what are the measures of central tendency in statistics, Measures of central tendency,Measures of Central Tendency & Examples
একাডেমিক শিক্ষা বিষয়ক লিখিত প্রশ্ন সমাধান পেতে ক্লিক করুন।
A measure of central tendency (also referred to as measures of centre or central location) is a summary measure that attempts to describe a whole set of data with a single value that represents the middle or centre of its distribution.
Measures of central tendency
Mean (Average): The mean is the sum of all values in a data set divided by the number of values. It is calculated using the formula:
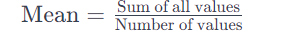
The mean is sensitive to extreme values (outliers) and may not accurately represent the center if the data set is skewed.
Median: The median is the middle value in a data set when it is arranged in numerical order. If there is an even number of observations, the median is the average of the two middle values. The median is less affected by extreme values than the mean and is a good measure of central tendency for skewed distributions.
Mode: The mode is the value that appears most frequently in a data set. A data set may have no mode, one mode (unimodal), or more than one mode (multimodal). Unlike the mean and median, the mode is not necessarily unique and may not exist in some data sets.
Measures of Central Tendency & Examples
A measure of central tendency (also referred to as measures of centre or central location) is a summary measure that attempts to describe a whole set of data with a single value that represents the middle or centre of its distribution.
There are three main measures of central tendency:
- mode
- median
- mean
Each of these measures describes a different indication of the typical or central value in the distribution.
Mode
The mode is the most commonly occurring value in a distribution.
Consider this dataset showing the retirement age of 11 people, in whole years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
This table shows a simple frequency distribution of the retirement age data.ImageDescription
Frequency distribution table
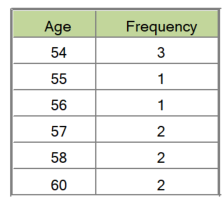
The most commonly occurring value is 54, therefore the mode of this distribution is 54 years.
Advantage of the mode
The mode has an advantage over the median and the mean as it can be found for both numerical and categorical (non-numerical) data.
Limitations of the mode
The are some limitations to using the mode. In some distributions, the mode may not reflect the centre of the distribution very well. When the distribution of retirement age is ordered from lowest to highest value, it is easy to see that the centre of the distribution is 57 years, but the mode is lower, at 54 years.
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
It is also possible for there to be more than one mode for the same distribution of data, (bi-modal, or multi-modal). The presence of more than one mode can limit the ability of the mode in describing the centre or typical value of the distribution because a single value to describe the centre cannot be identified.
In some cases, particularly where the data are continuous, the distribution may have no mode at all (i.e. if all values are different).
In cases such as these, it may be better to consider using the median or mean or group the data into appropriate intervals and find the modal class.
Median
The median is the middle value in distribution when the values are arranged in ascending or descending order.
The median divides the distribution in half (there are 50% of observations on either side of the median value). In a distribution with an odd number of observations, the median value is the middle value.
Looking at the retirement age distribution (which has 11 observations), the median is the middle value, which is 57 years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
When the distribution has an even number of observations, the median value is the mean of the two middle values. In the following distribution, the two middle values are 56 and 57, therefore the median equals 56.5 years:
52, 54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
Advantage of the median
The median is less affected by outliers and skewed data than the mean and is usually the preferred measure of central tendency when the distribution is not symmetrical.
Limitation of the median
The median cannot be identified for categorical nominal data, as it cannot be logically ordered.
Mean
The mean is the sum of the value of each observation in a dataset divided by the number of observations. This is also known as the arithmetic average.
Looking at the retirement age distribution again:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
The mean is calculated by adding together all the values (54+54+54+55+56+57+57+58+58+60+60 = 623) and dividing by the number of observations (11) which equals 56.6 years.
Advantage of the mean
The mean can be used for both continuous and discrete numeric data.
Limitations of the mean
The mean cannot be calculated for categorical data, as the values cannot be summed.
As the mean includes every value in the distribution the mean is influenced by outliers and skewed distributions.
Another thing about the mean
The population mean is indicated by the Greek symbol µ (pronounced ‘mu’). When the mean is calculated on a distribution from a sample it is indicated by the symbol x̅ (pronounced X-bar).
Impact of shape of distribution on measures of central tendency
Symmetrical distributions
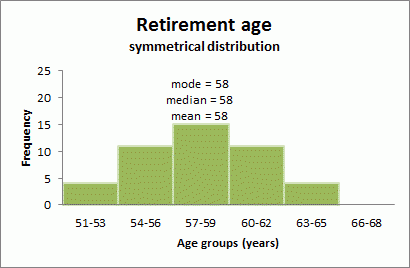
When a distribution is symmetrical, the mode, median and mean are all in the middle of the distribution. The following graph shows a larger retirement age dataset with a distribution which is symmetrical. The mode, median and mean all equal 58 years.ImageDescription
Retirement age: Symmetrical distribution
Skewed distributions
When a distribution is skewed the mode remains the most commonly occurring value, the median remains the middle value in the distribution, but the mean is generally ‘pulled’ in the direction of the tails. In a skewed distribution, the median is often a preferred measure of central tendency, as the mean is not usually in the middle of the distribution.
A distribution is said to be positively or right skewed when the tail on the right side of the distribution is longer than the left side. In a positively skewed distribution it is common for the mean to be ‘pulled’ toward the right tail of the distribution. Although there are exceptions to this rule, generally, most of the values, including the median value, tend to be less than the mean value.
The following graph shows a larger retirement age data set with a distribution which is right skewed. The data has been grouped into classes, as the variable being measured (retirement age) is continuous. The mode is 54 years, the modal class is 54-56 years, the median is 56 years, and the mean is 57.2 years.ImageDescription
Retirement age: Positive (right) skew

A distribution is said to be negatively or left skewed when the tail on the left side of the distribution is longer than the right side. In a negatively skewed distribution, it is common for the mean to be ‘pulled’ toward the left tail of the distribution. Although there are exceptions to this rule, generally, most of the values, including the median value, tend to be greater than the mean value.
The following graph shows a larger retirement age dataset with a distribution which left skewed. The mode is 65 years, the modal class is 63-65 years, the median is 63 years and the mean is 61.8 years.
central tendency in statistics
একাডেমিক শিক্ষা বিষয়ক লিখিত প্রশ্ন সমাধান পেতে ক্লিক করুন।
আর্টিকেলের শেষ কথাঃ central tendency in statistics, what are the measures of central tendency in statistics
Business statistics with answers to all questions
- What are the features of statistics? Answer: links
- What are the methods of collecting primary data? Answer: links
- Discuss the different types of scale of measurement. Answer: links
- Write the different steps of constructing a grouped frequency distribution. Answer: links
- Describe the functions of statistics Answer: links
- Honors 2nd Year Business Statistics Suggestion Answer: links
- what is Statistics, who is the father of modern statistics — Answer: links
- Discuss the importance of Statistics in Business —- Answer: links
- importance of statistics in management — Answer: links
- statistics in the main tool for the decision making of business explain — Answer: links
- Importance of statistics in decision-making — Answer: links
- write down the important characteristics of statistics — Answer: links
- What Are The Measures Of Central Tendency In Statistics — Answer: links






